Freshman

Project 1 - Graph Traversal Algorithms

Technology: Python, Visual Studio Code


		
			Question 1

		
		
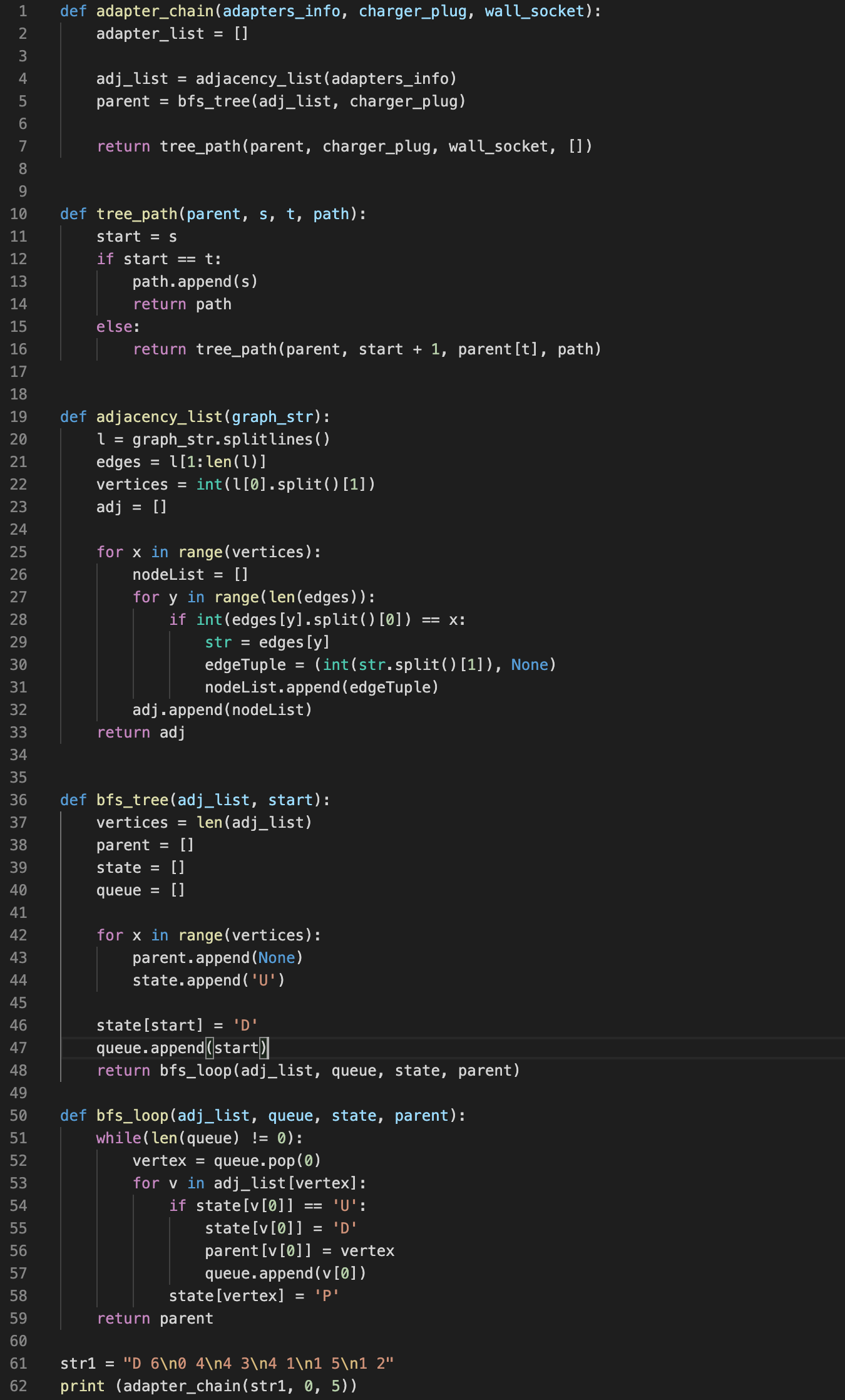
			For this, I implemented a breadth first search algorithm on a directed graph with the analogy of using wall outlet adapters. The scenario

			for the problem is that you are in a different country that uses a different type of wall outlet and you

			have a certain amount of different adapters with you that convert your charger's type to the wall outlet type.

			The algorithm outputs the least amount of adapters that you have to link together in order to convert your

			charger to the wall outlet.


		
		
			Graph Representation

		
		
			The strings at the bottom of the file represent the graph with the first character of the

			first line indicating whether the graph is directed (D) or undirected (U). The second character

			on the first line indicated how many nodes are in the graph. The rest of the lines indicate the edges,

			with the first number being the starting node and the second character being the ending node.

q1.py (click on image to download code):

Question 2

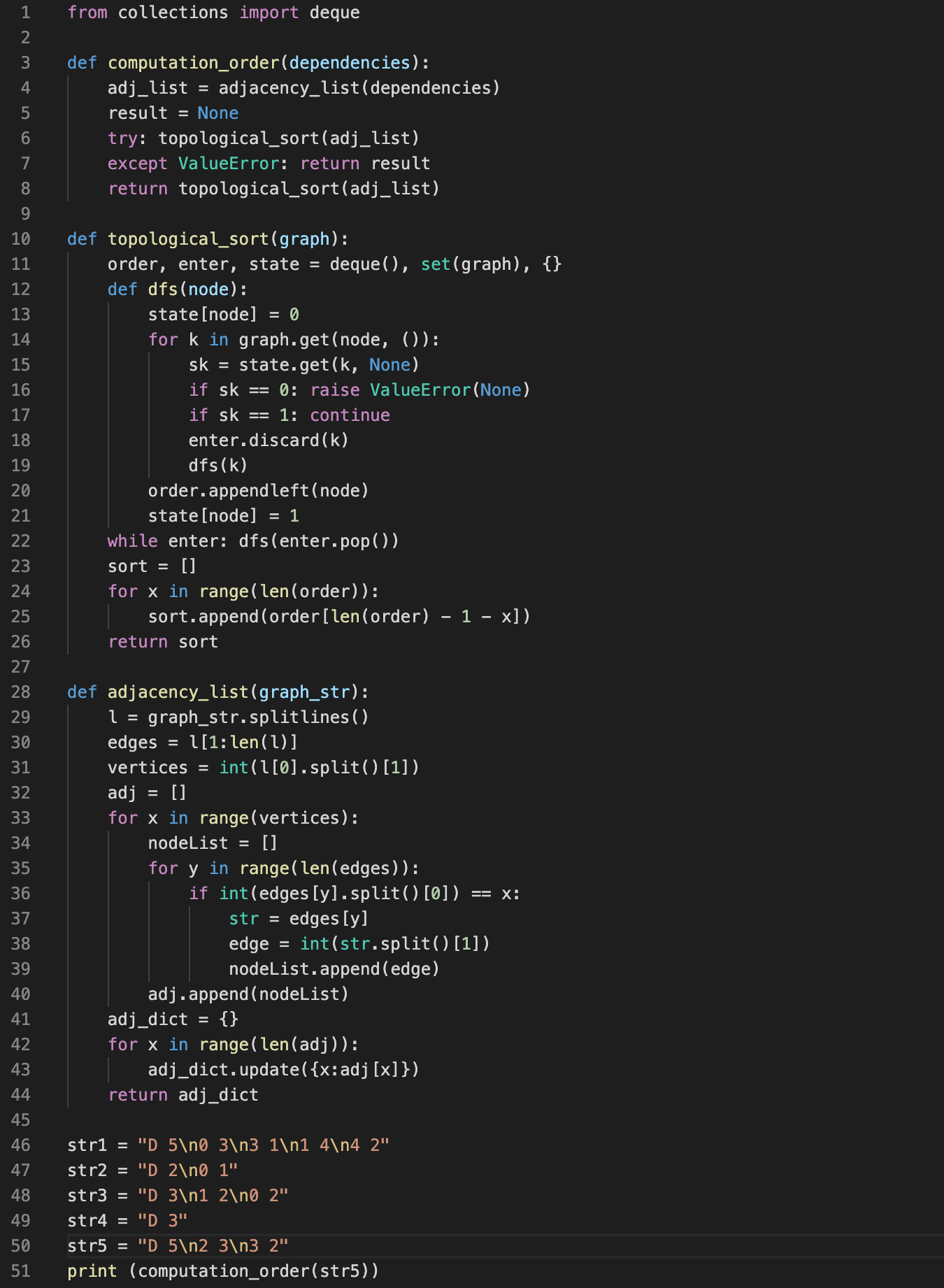
This algorithm performs a topological sort on a directed graph.

q2.py (click on image to download code):

Question 3

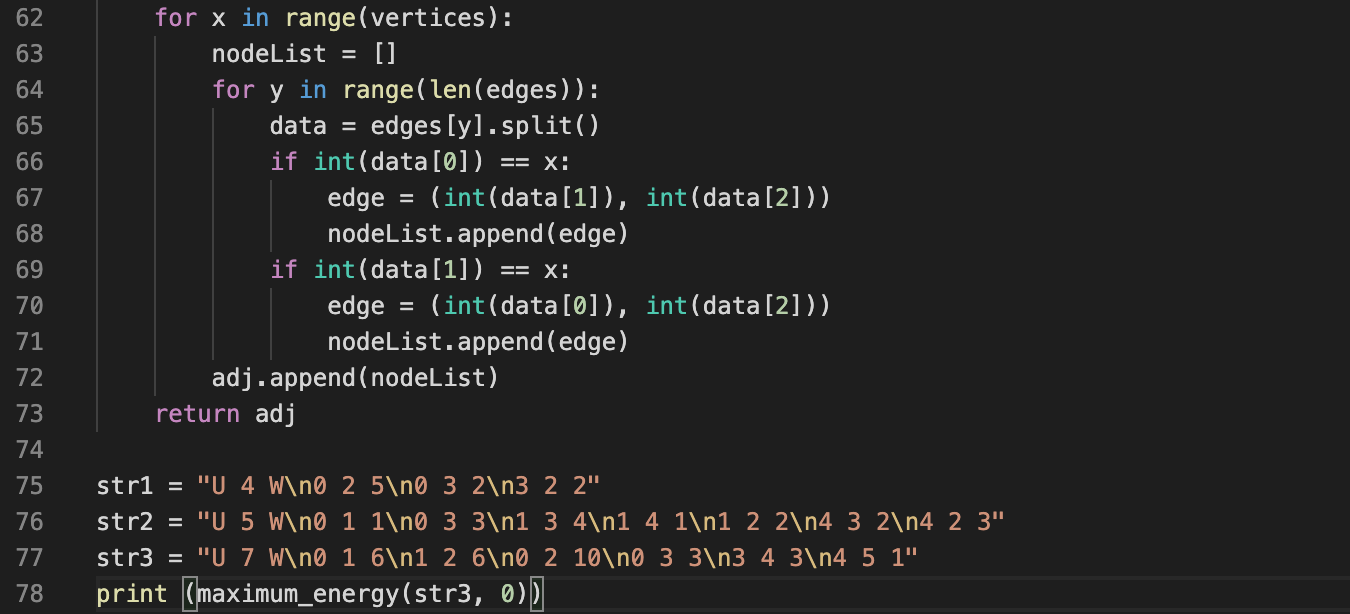
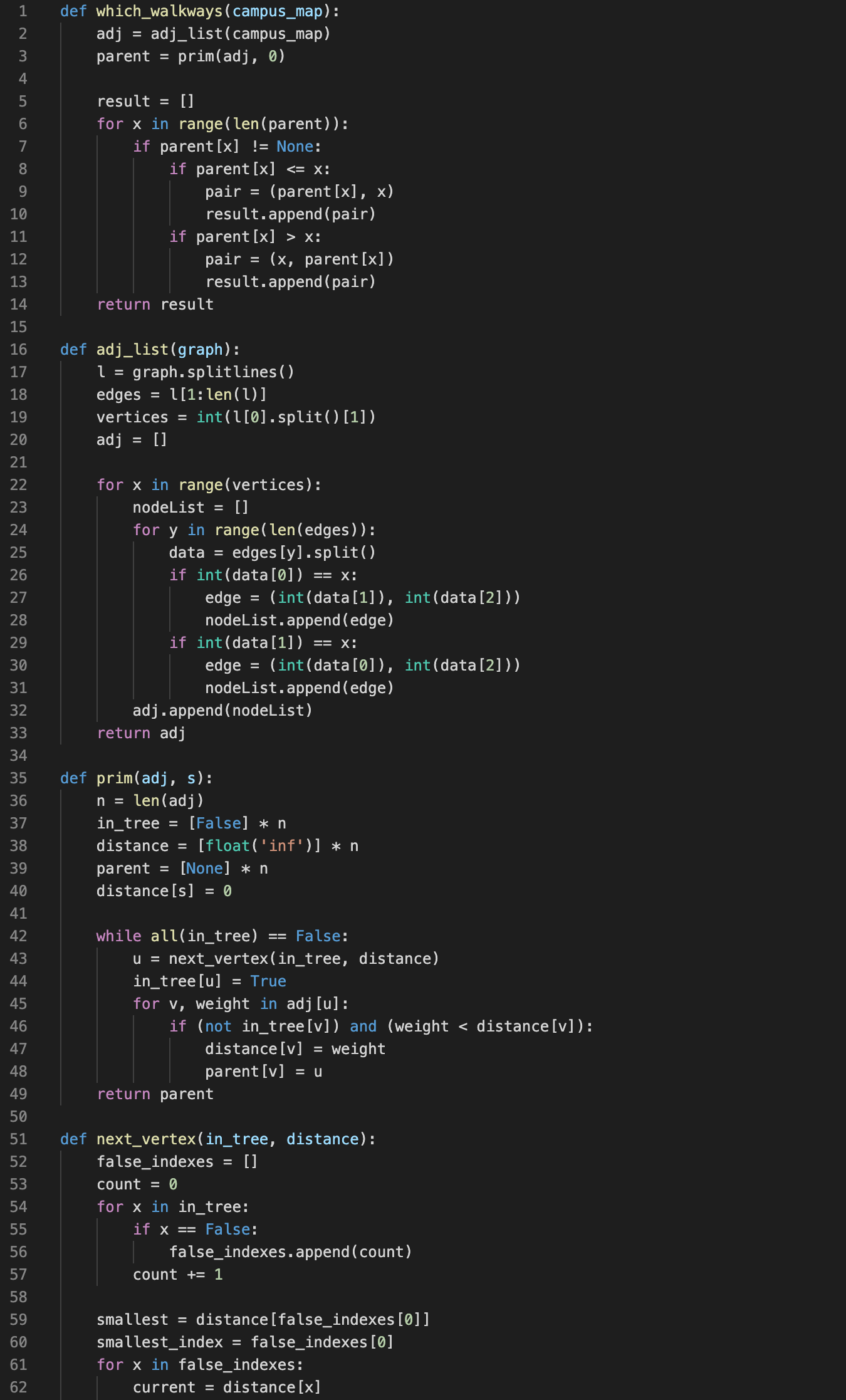
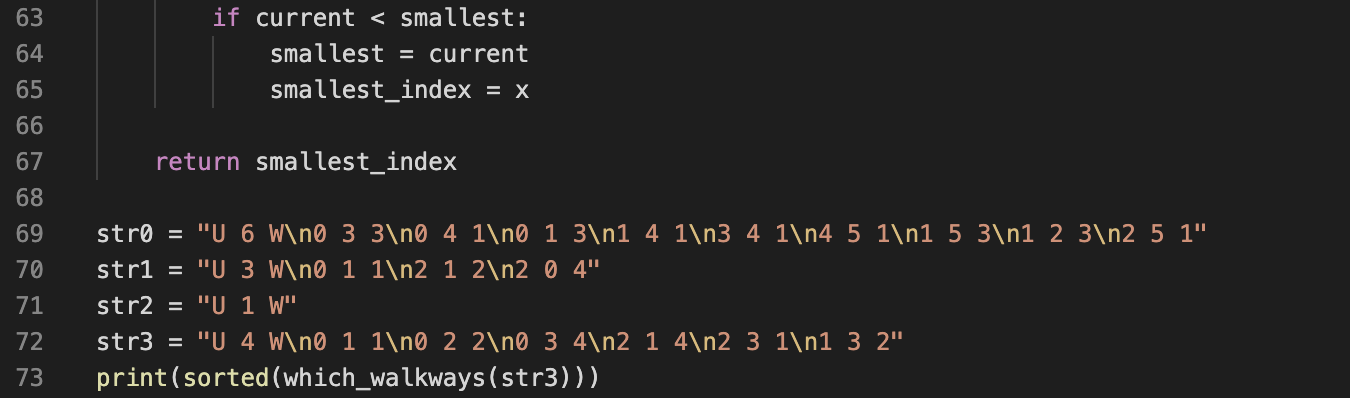
The scenario for this question is you are at a building on a college campus and you need to get
to another building via walkways taking the route with the least distance. The scenario uses an undirected
graph with the nodes being the buildings and the edges being the walkways. The graph representation is
the same as the directed graph's but there is a third number in each edge description which represents
the weight of the edge (walkway distance). The 'W' in the first line of the description indicates that
the graph is weighted. The algorithm finds the shortest path using Prim's algorithm.

q3.py (click on image to download code):

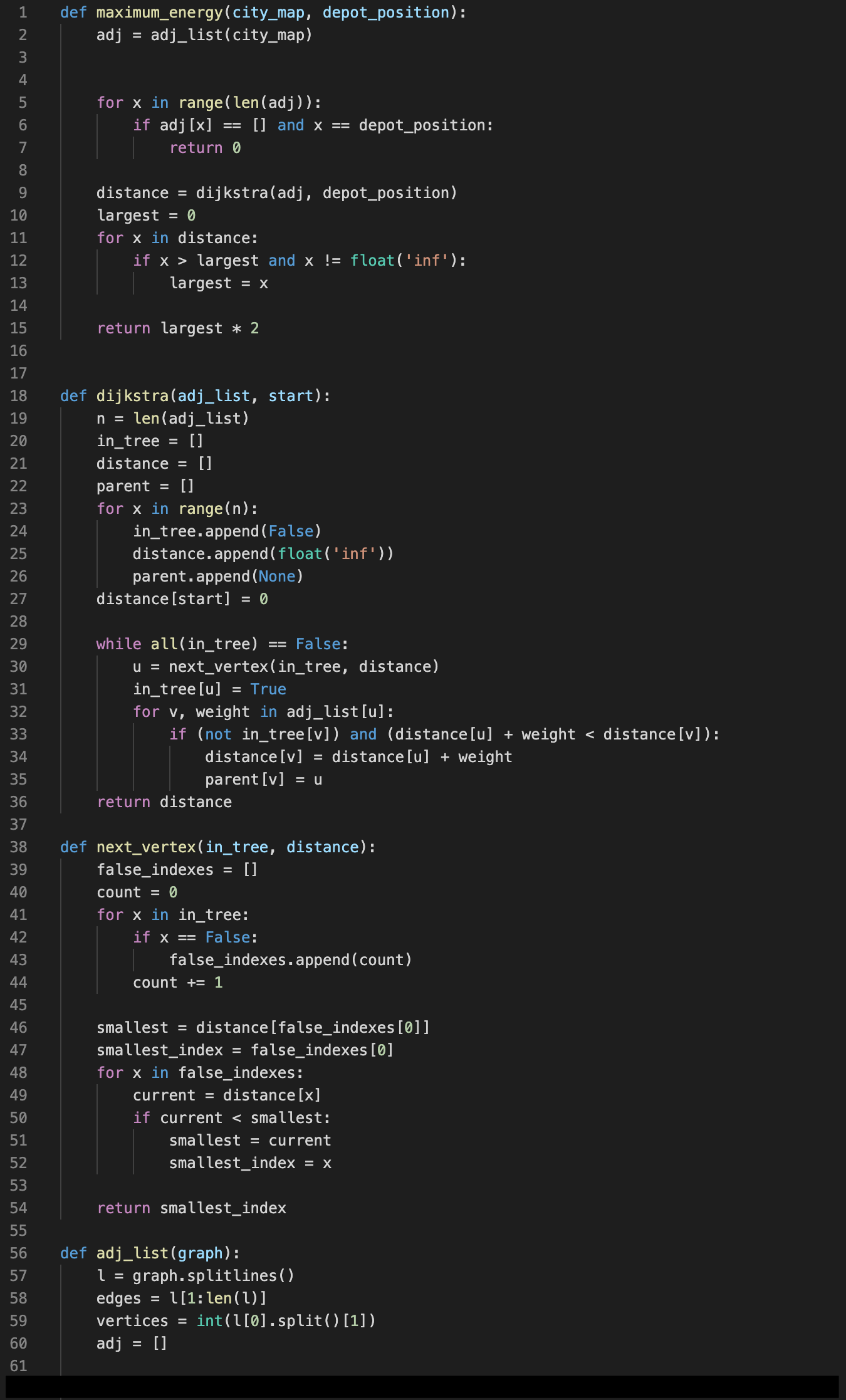
Question 4

This question uses Dijkstra's algorithm on an undirected weighted graph which is represented the
same way as the previous question. The algorithm find the shortest distances from a starting node
to every other node in the graph and returns the maximum of these distances.

q4.py (click on image to download code):